Matemáticas Discretas

Proyecto primer parcial

Eric Fernando Torres Rodríguez-A01700249
Ivan alejandro Díaz Peralta-A01700
Julio de Jesus Ramírez Fernández-A01705008

Proposiciones


Proposición:

Es una estructura compuesta por dos o más conceptos. Comprenden las unidades más pequeñas de las que se compone el procedimiento. Estas proponen algo, ya sea positivo o negativo el valor de la afirmación. En caso de ser compuestos, tienen una oración de enlace.[4]

Variable Proposicional:

Sibolos para las proposiciones

Proposiciones simples:

No se puede descomponer en hechos más simples.
  • Ejemplo:
La clase de OPP es sencilla.
El perro es grande.

Proposiciones compuestas:

Formadas por dos o más preposiciones primitivas.
  • Ejemplo:
La clase de OPP es sencilla e interactiva.
El día esta soleado y cálido.

Operadores Lógicos:

Negación, conjución, disyunción y disyunción exclusiva

Jerarquia de operadores:

Not And Or

Tablas de verdad:

Descripción organizada de los valores de verdad de la preposición para todos los valores posibles de la variables proposicionales que aparecen en ella.

Proposiciones imageProposiciones image

Leyes de equivalencia

FBF

FBF

Formula Bien Formada

Expresión que contiene variables proposicionales, constantes, operador lógico

Ejemplo:

  • p ∨ q
  • p ∨ (q ∧ ((¬r) ∧ s))
Más información  
Equivalencia Lógica

Equivalencia Lógica

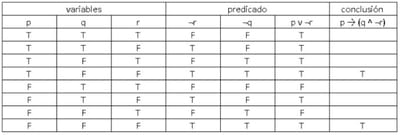
Dos proposiciones son lógicamente equivalentes cuando la primera proposición  es verdadera (o falsa en diferentes casos) si y solo si la segunda proposición  es verdadera (o falsa en diferentes casos).  Otra manera de definirlo es que dos formas proposicionales a y b son lógicamente equivalentes si y solo si tiene valores de verdad idénticos.[5]
Dos proposiciones pueden llamarse equivalentes cuando cada una de ellas implica a la otra. [3]

(Ejemplo en la imagen superior al texto)

Más información  
Ejemplo 1

Ejemplo 1

Ejemplo 2[1]

Ejemplo 2[1]

Condicional

La condicional es la forma proposicional más importante relacionado con la inferencia lógica [3]
 Si P, entonces Q
Decimos que p → q es verdadera cuando p es falsa, sin importar el valor de verdad de q.

Equivalencia básica de la condicional:
p → q ≡ ¬p ∨ q
reescribir en la forma “si.. entonces” el enunciado:
“O llega a tiempo al trabajo o lo despiden”.


Negación de la condicional:
¬(p → q) ≡ p ∧ ¬q

Existen otras condicionales que s epueden constuir a partir de una condicional original.

Si la condicional original se representa mediante p → q  las variantes quedarian de la siguiente manera.

Reciproca

La reciproca quedaria expresada de esta manera q → p

Inversa

La inversa quedaria expresada de esta manera ¬p →¬ q

Contrapositiva

La contrapositiva quedaria expresada de esta manera ¬q → ¬p

Ejemplos:

p=Hoy es viernes q=Mañana es sabado
Condicional (p → q): Si hoy es viernes, entonces mañana es sábado.
Reciproca (q → p): Si mañana es sábado, entonces hoy es viernes.
Inversa (¬p →¬ q): Si hoy no es viernes, entonces mañana no es sábado.
Contrapositiva (¬q → ¬p): Si mañana no es sábado, entonces hoy no es viernes.

p=Eric está triste q=Eric reprobo FIS
Condicional (p → q): Si Eric esta triste, entonces Eric reprobo FIS.
Reciproca (q → p): Si Eric reprobo FIS, entonces Eric esta triste.
Inversa (¬p →¬ q): Si Eric no esta triste, entonces Eric no reprobo FIS.
Contrapositiva (¬q → ¬p): Si Eric no reprobo FIS, entonces Eric no esta triste.


Condicional image

Bicondicional

Bicondicional image
La forma de proposición bicondicional “p ↔ q” p si y sólo si q, es verdadera si tanto p como q son verdaderas o falsas, importante el valor de ambas proposiciones. Tanto p como q. [3]
Ejemplos
  • P = la casa tiene jardín. Q = tiene un jardinero.
p ↔ q = la casa tiene jardín si solo si tiene un jardinero.

  • P = puede volar. Q = tiene alas.
p ↔ q = puede volar si solo si tiene alas.

  • P = hoy lloverá. Q = hay nubes grises.
p ↔ q = hoy lloverá si solo si hay nubes grises.

La equivalencia de una proposición bicondicional seria la conjunción de 2 condicionales tales que [3]
  • P ↔ Q = (P→Q) ^(Q→P)
Esto se podría reflejar en los ejemplos tomados anteriormente.
  • p ↔ q = la casa tiene jardín si solo si tiene un jardinero.
(P→Q) ^(Q→P) = si la casa tiene jardín entonces tiene un jardinero y si tiene un jardinero entonces la casa tiene jardín.

  • p ↔ q = puede volar si solo si tiene alas.
(P→Q) ^(Q→P) = si puede volar entonces tiene alas y si tienes alas entonces puede volar.

  • p ↔ q = hoy lloverá si solo si hay nubes grises.
(P→Q) ^(Q→P) = si hoy llueve entonces hay nubes grises y si hay nubes grises hoy llueve.

Argumento

Argumento image
Validación de un argumento
Para poder decir que un argumento es valido se tiene que tener tanto la premisa como la conclusión de forma valida. Para poder comprobar dicha cuestión se tienen que corroboras los permisos del predicado y cuando todas se constituyan verdad corroboramos la conclusión y si también resulta ser verdadera, podemos afirmar que es un argumento válido.[2]
O, dicho de otra manera, se realiza una tabla de verdad de los argumentos primero separándolo en sus variables de ahí sus predicados y por último en donde los predicados sean verdaderos comprobamos la conclusión.[2]
ejemplo
¬r
¬q
p v ¬r
∴ p → (q ^ ¬r)

Dado a la tabla de verdad podemos ver que la sentencia anterior es valida

Referéncias

1.-Botella(2017)Lógica equivalencia[Imagen].Recuperado de: https://slideplayer.es/slide/10291066/

2.-ITM. (2011,octubre,S.F). Argumentos validos y no validos. Matemáticas Discretas. Recuperado de: https://matedisunidad3.wordpress.com/category/3-1-7-argumentos-validos-y-no-validos/

3.- Johnsonbaugh., R. (2005). En Matemáticas discretas. México: PEARSON EDUCACIÓN.

4.- Miller. (2010,febrero,14). Qué es una proposición .cmap . Recuperado de: http://cmap.ihmc.us/docs/queesproposicion.html

5.- Susana. (2011,octubre,13). Equivalencias lógicas .Matematicas discretas . Recuperado de:https://matematicasdiscretasisc.wordpress.com/2011/10/13/equivalencias-logicas/



ESTE SITIO FUE CONSTRUIDO USANDO